Abstract
We present the solution to the Black Body Radiation worksheet problem 1, from week 3, recalling basic ideas of black body radiation from energy density to specific intensity and flux. In the first part, we investigate the contradiction of the units of energy density. In order to convert from energy density to intensity and flux, we have to study the concept of solid angle. These equations are used frequently in astronomy.
Introduction
A perfect blackbody object absorbs every electromagnetic radiation. From an energy it absorbed, a blackbody object is heated up and emits radiation corresponding to its specific temperature. Start with the energy density of radiation emitted from a blackbody, we can find the specific intensity and flux passed through a spherical surface. Constants that involved here are the Boltzmann’s constant and the Planck’s constant.
Solution
The energy density of radiation emitted from a blackbody is given by
where the Boltzmann's constant k=1.4 x 10^-16 ergs/K and the Planck's constant h=6.6 x 10^-27 erg s. From equation above, the second term on the right hand side is measured in the units of energy (ergs) while the first term is in the units of erg-seconds per volume. Thus, the units of the right hand side is erg-seconds per volume. However, the energy density should have a unit of erg per volume. The contradiction here is because the energy density here is "per frequency" so the unit is erg per volume per s^-1 or erg-seconds per volume as the equation suggested.
Before moving to a new topic, we have to investigate the idea of solid angle. "A solid angle is a differential element of the surface of a sphere, measured in spherical coordinates theta and phi, and expressed as omega. The units are steradians (pronounced 'stair-radians')" Next, we are going to calculate the whole solid angle of a sphere.
From a diagram above, we can represent dy and dx in term of r, theta, and phi.
From these equations, we can find the solid angle of the small patch.
In order to find the solid angle of the whole sphere, we integrate theta from zero to pi and phi from zero to 2pi.
The specific intensity, B(T), from a black body is the flow of photons through all solid angles. In order to get to the specific intensity, we differentiate the energy density with respect to solid angle and multiplying by c. Since the radiation is isotropic, the differentiation with respect to solid angle is the same as divide it by the whole solid angle or 4pi.
The flux is the projection of the specific intensity in the radial direction by integrate over all solid angles.
Now, since the specific intensity does not depend on the angle.
Acknowledgement
We thank Prof. Johnson and Jackie for advices. The definition of solid angle is taken from the worksheet. The diagram for solid angle is drawn by me and scanned by the scanner at my bedroom. All equation are made by online LaTex editor.




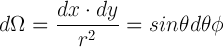



No comments:
Post a Comment