Abstract
We present how the radius of the Earth could be measured using only a stopwatch and a place where the horizon can be seen, e.g. beach. A stopwatch and a difference in height provide the curvature of the Earth by watching a sunset and assuming that the Earth is a perfect sphere. Since a person’s height is much less than the radius of the Earth, one small error in a measurement could mean a large inaccuracy in the final answer.
Introduction
After the belief in spherical earth substituted the paradigm of flat earth, many scientists in ancient time tried to measure the radius of the Earth. Some of them made a nearly accurate measurement of the radius of the Earth using only two sticks and an observation of the Sun. Moreover, the radius of the Earth is used to calculate other astronomical constants such as the astronomical unit (AU) or a distance from earth to the sun etc. An accurate measurement of the radius of the Earth can be found easily on the Internet but in this experiment, we used only a stopwatch trying to make a precise measurement.
Radius of the Earth Calculation
Before we went to the Santa Monica beach, we figured out how to calculate the radius of the Earth using geometry. When the sun is about to set, an experimenter lays down looking toward the west horizon. It is safe to look at the sun with naked eyes but only during the sunrise or sunset. Figure 1 shows a diagram of an experimenter laying down on the Earth’s surface. He/she sees the sun set completely when his head is in the shadow of the Earth. At that time, the experimenter starts the stopwatch and stands up without moving away from the laying spot. With the extra height from standing up, the experimenter will magically see the sun once again because his head gets out from the Earth’s shadow (Figure 2.)
Figure 1 - The experimenter lays down on the Earth's surface waiting for the sun to set and start the stopwatch.
Figure 2 - The experimenter stands up and magically sees the sun once again because of the extra height.
Without changing the position, the experimenter waits for the Sun to disappear again caused by the rotation of the Earth. Then, he/she would stop the stopwatch. In figure 3, the experimenter sees the sun disappeared for the second time because the earth rotates with an angle theta.
Figure 3 - After some time, the experimenter sees the sun disappeared again because of the rotation of the Earth with and angle theta. The experimenter stops the stopwatch and get the elapsed time.
From the elapsed time, we could figure out the angle the Earth rotates by the following relationship,
where the elapsed time is in second and the theta is in degree. In figure 3, the triangle OAB can be used to calculate the radius of the Earth by using the geometry of cosine.
In the real experiment, we made the measurement two times - when the bottom part of the sun touches the horizon and when the sun is completely disappeared. During the first experiment, because of the Earth's atmosphere, it was hard to tell whether the Sun has touched the horizon. With my height of 1.7 meter, the elapsed time turns out to be 8 seconds.
Similarly, the second experiment yields the elapsed time of 6 second.
From two numbers of the radius of the Earth, we can calculate the mean value and the deviation.
Summary and Discussion
From Wolfram Alpha, the average radius of the Earth is 6367.5 km. Thus, the result from the experiment is just an order of magnitude off and it is almost twice an official value. One possible error is the difference in judgement of two people. In the experiment, the person who lays down and stands up is no the same person. The judgements on whether the sun has touched the horizon or whether the sun has disappeared between these two people might be different. Thus, the base line for starting and stopping the timer are not the same. Moreover, the Earth's atmosphere makes the horizon not a clear cut line.
Acknowledgements
We thank all drivers who took us to the Santa Monica beach. We used WolframAlpha to get an official value for the radius of the Earth to compare with our experimental result. Also, we thank Iryna for laying down on the sand. Figure 1, 2, and 3 are drawn by me and scanned at the SFL copy machine number 4. The equations were generated using CodeCogs online LaTex editor.



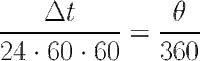







GREAT blog entry, Mee! I really like how you explained why the Sun disappears later for someone who is standing up. The pictures are wonderful!
ReplyDeleteGr8 experiment.
ReplyDeletethese calculations don't work
ReplyDeleteVery high margin of error...
ReplyDelete